该比赛已结束，您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。

Statement

Homeward-bound during the flowers' season, I dread to see them fade; Through endless flames of war, the journey is hard and delayed. How much regret has the spring wind witnessed, in vain? To whom could I entrust a solitary bloom, for whom to view and retain?

As spring returns, traveler Paper passes through a war-torn region. Seeing a tree in full bloom, she worries about its withering. The ongoing war and the perilous roads mean that storing an entire tree would be prohibitively expensive—a cost determined by the longest path between branches (i.e., the tree's diameter^[1]). To preserve the beauty of spring, Paper wants to send a flower as a token of her feelings, but a tree with a long diameter is vulnerable to loss. She can employ a clever trick: select a branch path (e.g., from starting point $s$ to end point $t$), shift its edges, and then tie all branches along the path (except the starting point) directly to starting point $s$, making the path as compact as a new branch without any loss. This way, the tree remains a tree, but its path is shortened. Please help Paper find the minimum number of operations required to minimize the diameter, so that she can express her regret for the spring wind and preserve the beauty of spring.

Spring arrives, and Paper wants to store a tree. She knows that the cost of storing it depends on the tree's diameter. The diameter of a tree is the longest possible distance between any pair of vertices, which is itself measured by the number of edges on the unique simple path connecting them. To reduce storage space without breaking branches, her goal is to first minimize the diameter. She can do the following for the tree:

• Take two vertices $s$ and $t$, and let the simple path^[2] from $s$ to $t$ be The vertex sequence on it is $v_0, v_1, \dots, v_k$, where $v_0 = s$ and $v_k = t$;
• Remove all edges on the path; in other words, remove the edges $(v_0, v_1), (v_1, v_2), \dots, (v_{k-1}, v_k)$;
• Connect vertices $v_1, v_2, \dots, v_k$ directly to $v_0$. In other words, add the edge $(v_0, v_1), (v_0, v_2), \dots, (v_0, v_k)$.

It can be shown that after the above operations, the graph is still a tree. Please help her determine the minimum number of operations required to achieve the minimum diameter.

Input

Each test contains multiple test cases. The first line contains the number of test cases, $t$ ($1 \leq t \leq 10^4$). The test cases are described as follows:

The first line of each test case contains an integer, $n$ ($2 \le n \le 2 \cdot 10^5$), representing the number of nodes in the tree. The next $n-1$ lines of each test case describe a tree: each line contains two integers, $u$ and $v$ ($1 \le u, v \le n$, $u \neq v$), representing the edges between vertices $u$ and $v$, and ensuring that these edges form a tree.

The sum of $n$ across all test cases is guaranteed to be no more than $2 \cdot 10^5$. The next $n-1$ lines of each test case describe a tree. Each line contains two integers $u$ and $v$ (where $1 \le u, v \le n$, $u \neq v$), representing an edge between vertices $u$ and $v$. These edges are guaranteed to form a tree.

The sum of $n$ across all test cases is guaranteed to not exceed $2 \cdot 10^5$.

Output

For each test case, output an integer representing the minimum number of operations required to minimize the diameter.

Samples

4
4
1 2
1 3
2 4
2
2 1
4
1 2
2 3
2 4
11
1 2
1 3
2 4
3 5
3 8
5 6
5 7
7 9
7 10
5 11
 

1
0
0
4

Notes

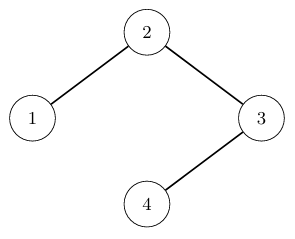
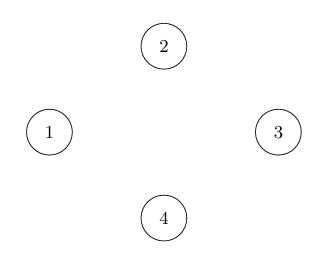
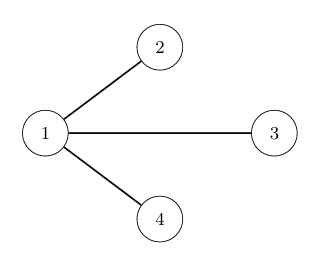
In the first test case, the original tree has a diameter of 3. Paper can perform the operation on $s = 1$ and $t = 4$. As shown in the figure, the operation consists of the following steps:

1. Remove tree paths $(1, 2)$, $(2, 3)$, and $(3, 4)$.

2. Added tree paths $(1, 2)$, $(2, 3)$, and $(3, 4)$.

After the above operations, the diameter is reduced to $2$. It can be shown that $2$ is the minimum diameter.

In the second example, the diameter of the tree is 1. It can be shown that 1 is already the minimum value, so Paper does not need to perform any operations.